Bloom Filter是一种空间效率很高的概率型数据结构,由位数组和一组哈希函数组成。特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”。总体规则是:位数组中存放的是:集合中每个元素的哈希转二进制后对应的值,对于新加入的元素根据其哈希值去判断是否已经存在于集合中。
结构
Bloom Filter使用位数组来实现过滤,初始状态下位数组每一位都为0,如下图所示:

假如此时有一个集合S = {x1, x2, … xn},Bloom Filter使用k个独立的hash函数,分别将集合中的每一个元素映射到{1,…,m}的范围。对于任何一个元素,被映射到的数字作为对应的位数组的索引,该位会被置为1。比如元素x1被hash函数映射到数字8,那么位数组的第8位就会被置为1。下图中集合S只有两个元素x和y,分别被3个hash函数进行映射,映射到的位置分别为(0,3,6)和(4,7,10),对应的位会被置为1:
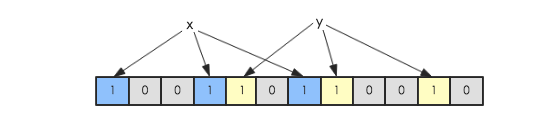
现在假如要判断另一个元素是否是在此集合中,只需要被这3个hash函数进行映射,查看对应的位置是否有0存在,如果有的话,表示此元素肯定不存在于这个集合,否则有可能存在。下图所示就表示z肯定不在集合{x,y}中:
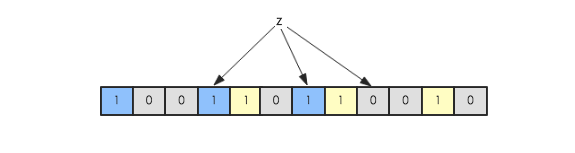
对有可能存在的解释
假设X进行三次hash后对应的bit位是(0,3,6),Y被三次hash后对应的bit位是(0,3,7),则Y在bit的0和3的值会覆盖掉X的值,假设还有一个新元素Z的hash结果是(1,3,6),则意味着X的hash结果被全部覆盖,也就是说即使没有X,(0,3,6)位置的值也是1,所以只能是有可能存在。
CBF
由于判断某个元素在bloom filter是否存在时个概率问题,所以就不能随便删除一个元素了,如上如果我们删除了X元素的哈希结果,那么Y元素和Z元素也会被误判为不存在集合中。
删除元素问题可以通过布隆过滤器的变体CBF(Counting bloomfilter)解决。CBF将基本Bloom Filter每一个Bit改为一个计数器,这样就可以实现删除字符串的功能了。
它将标准Bloom Filter位数组的每一位扩展为一个小的计数器(Counter),在插入元素时给对应的k(k为哈希函数个数)个Counter的值分别加1,删除元素时给对应的k个Counter的值分别减1。Counting Bloom Filter通过多占用几倍的存储空间的代价,给Bloom Filter增加了删除操作。
其他bloomfilter的升级版:
SBF(Spectral Bloom Filter):在判断元素是否存在的基础上还可以查询集合元素的出现频率。dlCBF(d-Left Counting Bloom Filter):利用 d-left hashing 的方法存储 fingerprint,解决哈希表的负载平衡问题;ACBF(Accurate Counting Bloom Filter):通过 offset indexing 的方式将 Counter 数组划分成多个层级
应用场景
- 网页爬虫对URL的去重,避免爬取相同的URL地址;
- 反垃圾邮件,从数十亿个垃圾邮件列表中判断某邮箱是否垃圾邮箱(同理,垃圾短信);
- 缓存击穿,将已存在的缓存放到布隆中,当黑客访问不存在的缓存时迅速返回避免缓存及DB挂掉。
- spark的jion操作中
Runtime Filter的过滤原理实现。
数学结论
http://blog.csdn.net/jiaomeng/article/details/1495500该文中从数学的角度阐述了布隆过滤器的原理,以及一系列的数学结论。
首先,与布隆过滤器准确率有关的参数有:
- 哈希函数的个数k;
- 布隆过滤器位数组的容量m;
- 布隆过滤器插入的数据数量n;
主要的数学结论有:
- 为了获得最优的准确率,当k = ln2 * (m/n)时,布隆过滤器获得最优的准确性;
- 在哈希函数的个数取到最优时,要让错误率不超过є,m至少需要取到最小值的1.44倍;
参考
https://zhuanlan.zhihu.com/p/43263751
https://blog.csdn.net/tianyaleixiaowu/article/details/74721877

